#متتالية_فيبوناتشي أو #أعداد_فيبوناتشي نسبة إلى ليوناردو #فيبوناتشي ، وتعرف رياضاتياً بأنها الأرقام التي تكون في #المتتالية التالية :

بتعريفها فإن أول من أرقام فيبوناتشي هما 0 و 1، ويكون كل رقم هو نتاج مجموع الرقمين السابقين له. بعض المدارس حذفت الرقم 0 الأساسي واستبدلته بالرقم 1 مرتين.
تعرف المتتالية Fn لرقم فيبوناتشي بالوصف الرياضياتي بالعلاقة المتكررة
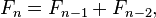
مع القيم الناتجة منها
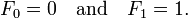
-------------------------------
سميت #متتالية فيبوناتشي نسبة إلى ليوناردو البيسي والمعروف باسم فيبوناتشي (باللاتينية: Fibonacci) وتعني ابن بوناشيو filius Bonaccio.
وكتابه الذي ألفه سنة 1202 واسمه ليبري أباتشي حيث عرف المتتالية في رياضيات الغرب الأوروبي، وقد كانت تلك المتتالية معروفة وموصوفة بالسابق في الرياضيات الهندية .
استخدمت أرقام فيبوناتشي في تحليل الأسواق المالية، في استراتيجيات مثل ارتداد فيبوناتشي وفي خوارزميات االكمبيوتر مثل تقنية فيبوناتشي للبحث وهيكلة بيانات تكدس فيبوناتشي .
وهي تظهر أيضا في الترتيبات البيولوجية، مثل تفريعات الأشجار، ترتيب الأوراق على الساق وطرف الثمرة من الأناناس وتفتح الخرشوف والسرخس غير المتجعد وترتيب مخروط الصنوبر .
---------------------------------------------------
الأصول
عرف الهنود القدماء متتالية فيبوناتشي قبل ظهورها في أوروبا، حيث طبقوها في علم أوزان الشعر.
وجاء الدافع لذلك من العروض السنسكريتية، حيث المقاطع الطويلة لها فترة = 2 والمقاطع القصيرة لها فترة = 1. يمكن تشكيل أي نمط له فترة ن وذلك بإضافة مقطع قصير إلى نمط من فترة ن − 1، أو مقطع طويل لنمط من فترة (( ن − 2 )) ، وبالتالي فإن عروض الشعر تظهر أن عدد أنماط فترة ن هو مجموع الرقمين السابقين من التسلسل. وبعد ذلك بدأ المؤلفون باستخدام الخوارزميات لتصنيف أو عدم تصنيف تلك الأنماط (بمعنى إيجاد النمط المرقم بالكاف من الفترة ن)، مما أدى لاكتشاف أرقام فيبوناتشي عليا. وقد استعرض دونالد كانوث تلك النتيجة في كتابه فن برمجة الحاسوب.
.
وقد بدأ ليوناردو البيسي المعروف باسم فيبوناتشي بدراسة تلك المتتالية في أوروبا في كتابه ليبر أباتشي . واعتبر النمو على افتراض (وهو غير صحيح في علم الأحياء) مجموعة ارانب كالتالي: حقل به زوج من الأرانب حديثي الولادة إحداهما ذكر والآخر انثى، فالأرانب بإمكانها التزاوج عند بلوغ الشهر، لذا ففي نهاية الشهر التالي تكون الأنثى قد ولدت زوج من الأرانب؛ بافتراض أنه لم يمت أي أرنب خلال مدة معينة وبافتراض أن في كل شهر ينتج زوج من الأرانب (ذكر وأنثى) بدأ من الشهر التالي. فكان اللغز الذي طرحه فيبوناتشي هو: كم سيكون عدد الأزواج في السنة الواحدة؟
* في نهاية الشهر الأول سيحصل تزاوج، ولكن يبقى أن هناك زوجا واحدا فقط.
* في نهاية الشهر التالي، الأنثى تلد زوجا جديدا، لذا سيكون هناك زوجين من الأرانب في الحقل.
* في نهاية الشهر الثالث، الأنثى الأصل تلد زوجا جديدا، مما يصبح العدد هو 3 أزواج من الأرانب في الحقل.
* في نهاية الشهر الرابع الأنثى الأصل تلد زوجا من الأرانب، والأنثى التي ولدت قبل شهرين تلد أول زوج لها من الأرانب. مما يصبح العدد هو 5 أزواج.
وفي نهاية المطاف عند الشهر ن، عدد الأزواج من الأرانب يساوي عدد الأزواج المواليد (حيث هو عدد الأزواج في الشهر ن-2) زائد عدد الأزواج الأحياء عند آخر شهر. هذا هو أو العدد ن لمتتالية فيبوناتشي
وفي نهاية المطاف عند الشهر ن، عدد الأزواج من الأرانب يساوي عدد الأزواج المواليد (حيث هو عدد الأزواج في الشهر ن-2) زائد عدد الأزواج الأحياء عند آخر شهر. هذا هو أو العدد ن لمتتالية فيبوناتشي[11].
-----------------------------------------------------
الصيغة العامة لمتتالية فيبوناتشي :
الصيغة العامة لمتتالية فيبوناتشي هي :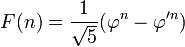
حيث
وحيث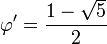
.
و هذه بعض القيم: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,...
ويقترب ناتج قسمة كل رقم بما قبله من 1.618 شيئا فشيئا للرقم الذهبي ويسمى هذا الرقم أيضا برقم التناسب المقدس والنسبة الذهبية.
----------------------------------------------------------------------------------------
المقال الأصلي عن الموسوعة الحرة ويكيبيديا - بتصرف وبعض التعديل

بتعريفها فإن أول من أرقام فيبوناتشي هما 0 و 1، ويكون كل رقم هو نتاج مجموع الرقمين السابقين له. بعض المدارس حذفت الرقم 0 الأساسي واستبدلته بالرقم 1 مرتين.
تعرف المتتالية Fn لرقم فيبوناتشي بالوصف الرياضياتي بالعلاقة المتكررة
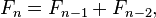
مع القيم الناتجة منها
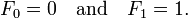
-------------------------------
سميت #متتالية فيبوناتشي نسبة إلى ليوناردو البيسي والمعروف باسم فيبوناتشي (باللاتينية: Fibonacci) وتعني ابن بوناشيو filius Bonaccio.
وكتابه الذي ألفه سنة 1202 واسمه ليبري أباتشي حيث عرف المتتالية في رياضيات الغرب الأوروبي، وقد كانت تلك المتتالية معروفة وموصوفة بالسابق في الرياضيات الهندية .
استخدمت أرقام فيبوناتشي في تحليل الأسواق المالية، في استراتيجيات مثل ارتداد فيبوناتشي وفي خوارزميات االكمبيوتر مثل تقنية فيبوناتشي للبحث وهيكلة بيانات تكدس فيبوناتشي .
وهي تظهر أيضا في الترتيبات البيولوجية، مثل تفريعات الأشجار، ترتيب الأوراق على الساق وطرف الثمرة من الأناناس وتفتح الخرشوف والسرخس غير المتجعد وترتيب مخروط الصنوبر .
---------------------------------------------------
الأصول
عرف الهنود القدماء متتالية فيبوناتشي قبل ظهورها في أوروبا، حيث طبقوها في علم أوزان الشعر.
وجاء الدافع لذلك من العروض السنسكريتية، حيث المقاطع الطويلة لها فترة = 2 والمقاطع القصيرة لها فترة = 1. يمكن تشكيل أي نمط له فترة ن وذلك بإضافة مقطع قصير إلى نمط من فترة ن − 1، أو مقطع طويل لنمط من فترة (( ن − 2 )) ، وبالتالي فإن عروض الشعر تظهر أن عدد أنماط فترة ن هو مجموع الرقمين السابقين من التسلسل. وبعد ذلك بدأ المؤلفون باستخدام الخوارزميات لتصنيف أو عدم تصنيف تلك الأنماط (بمعنى إيجاد النمط المرقم بالكاف من الفترة ن)، مما أدى لاكتشاف أرقام فيبوناتشي عليا. وقد استعرض دونالد كانوث تلك النتيجة في كتابه فن برمجة الحاسوب.
.
وقد بدأ ليوناردو البيسي المعروف باسم فيبوناتشي بدراسة تلك المتتالية في أوروبا في كتابه ليبر أباتشي . واعتبر النمو على افتراض (وهو غير صحيح في علم الأحياء) مجموعة ارانب كالتالي: حقل به زوج من الأرانب حديثي الولادة إحداهما ذكر والآخر انثى، فالأرانب بإمكانها التزاوج عند بلوغ الشهر، لذا ففي نهاية الشهر التالي تكون الأنثى قد ولدت زوج من الأرانب؛ بافتراض أنه لم يمت أي أرنب خلال مدة معينة وبافتراض أن في كل شهر ينتج زوج من الأرانب (ذكر وأنثى) بدأ من الشهر التالي. فكان اللغز الذي طرحه فيبوناتشي هو: كم سيكون عدد الأزواج في السنة الواحدة؟
* في نهاية الشهر الأول سيحصل تزاوج، ولكن يبقى أن هناك زوجا واحدا فقط.
* في نهاية الشهر التالي، الأنثى تلد زوجا جديدا، لذا سيكون هناك زوجين من الأرانب في الحقل.
* في نهاية الشهر الثالث، الأنثى الأصل تلد زوجا جديدا، مما يصبح العدد هو 3 أزواج من الأرانب في الحقل.
* في نهاية الشهر الرابع الأنثى الأصل تلد زوجا من الأرانب، والأنثى التي ولدت قبل شهرين تلد أول زوج لها من الأرانب. مما يصبح العدد هو 5 أزواج.
وفي نهاية المطاف عند الشهر ن، عدد الأزواج من الأرانب يساوي عدد الأزواج المواليد (حيث هو عدد الأزواج في الشهر ن-2) زائد عدد الأزواج الأحياء عند آخر شهر. هذا هو أو العدد ن لمتتالية فيبوناتشي
وفي نهاية المطاف عند الشهر ن، عدد الأزواج من الأرانب يساوي عدد الأزواج المواليد (حيث هو عدد الأزواج في الشهر ن-2) زائد عدد الأزواج الأحياء عند آخر شهر. هذا هو أو العدد ن لمتتالية فيبوناتشي[11].
-----------------------------------------------------
الصيغة العامة لمتتالية فيبوناتشي :
الصيغة العامة لمتتالية فيبوناتشي هي :
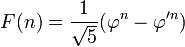
حيث

وحيث
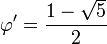
.
و هذه بعض القيم: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,...
ويقترب ناتج قسمة كل رقم بما قبله من 1.618 شيئا فشيئا للرقم الذهبي ويسمى هذا الرقم أيضا برقم التناسب المقدس والنسبة الذهبية.
----------------------------------------------------------------------------------------
المقال الأصلي عن الموسوعة الحرة ويكيبيديا - بتصرف وبعض التعديل





» أنشطة ضرورية لحياة جامعية أكثر متعة وفائدة
» تحليل عقدي 2 سلالم ودورات من 2014 حتى 2016 فصل أول
» معادلات فيزيائية سلالم تصحيح من 2009 وحتى 2014
» فريق جامعة البعث بالميني فوتبول بطل الجامعات 2016
» امتحانات جامعة البعث الفصل الثاني 2016
» دليل أفكار البنى الجبرية 2
» بنى جبرية 2 - سلالم تصحيح
» حدسية بوانكاريه
» غربال إراتوستينس
» نظرية الشواش
» طبولوجيا مدخل وتعريف