#المتتالية
أيضاً تسمى #المتتابعة و #المتوالية والتناسب .
تعريفها : هي مجموعة من الأغراض أو الأحداث المرتبة بنمط خطي حيث يكون ترتيب أعضاء المتتالية محددا تماما ومميزا. هذه الأعضاء تسمى عناصر المتتالية أو حدودها.
-----------------
تعريف رياضي : تسمى كل #دالة معرفة على مجموعة الأعداد الطبيعية متتالية .
فإذا كنا مستقر هذه التطبيق مجموعة الأعداد الحقيقية R سميت متتالية حقيقية .
وإذا كنا مستقر هذه التطبيق مجموعة الأعداد العقدية C سميت متتالية عقدية .
أما في مجموعة الدوال فتسمى متتالية دالية أو متتالية دوال .... وهكذا .
-----------------
مثلا (أ، ب، ج) متتالية مختلفة عن (ب، ج، أ) والاختلاف أساسا هنا هو في ترتيب عناصر المتتالية.
يمكن للمتتالية أن تكون منتهية كما هو الحال في المثال السابق أو غير منتهية مثل متتالية الأعداد الطبيعية : 1، 2، 3،...
------------------
#المتتاليات_العددية :
يمكن أن تعتبر المتتالية أيضا دالة رياضية منطلقها مجموعة الأعداد الطبيعية ومستقرها مجموعة عناصر المتتالية :
بمعنى أنها دالة تربط كل عنصر في مجموعة ما بترتيب معين يدل عليه عدد طبيعي : (f : N → X)
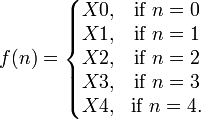
.
بهذا نكون قد قمنا عن طريق الدالة بترتيب أعضاء المجموعة X حسب الترتيب x0x1,x2...., حيث تدعى الأعداد 0، 1، 2،... دليل المتتالية.
----------------------------------------------------------
نرمز للمتالية بحرف بين قوسين مثل (a) .
يسمى a1 الحد الأول للمتتالية .
ويسمى a2 الحد الثاني للمتالية . .....
..... وهكذا
حتى نصل إلى an الحد العام للمتالية أو الحد النوني .
---------------------------------------------------------
#المتتالية_الحسابية :
في الرياضيات، متتالية حسابية هي متتالية من الأعداد حيث يكون الفرق بين أي حدين متتالين ثابتا.
على سبيل المثال فإن 3، 5، 7، 9، 11، 13، … هي متتالية حسابية لها أساس يساوي 2. أي أنّ 3، 5، 7 هي حدود من هذه المتتالية و الأساس 2 هو العدد المضاف بين كل حدّين متتاليين.
إذا كان الحد الأول من المتتالية الحسابية هو a1 و الفرق بين حدين متتاليين هو d عندها يعبر عن الحد ذي الترتيب n من متتالية حسابية بالعلاقة التالية:

أو بشكل عام

مثال
المتتالية 1 ،-3 ،-7، -11,.... حدها الأول هو 1 وأساسها هو 4- لأن الفرق بين حدين متتابعين يساوي دائما 4. وحتى نحصل على d نطرح كل حد من سابقه كالتالي:

لايجاد الحد النوني العشرين على سبيل المثال، تُطبق المعادلة السابقة :
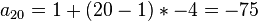
--------------------------------------------------
مجموع متتالية حسابية : (مهم جدا لمعرفة تقارب أو تباعد المتتالية لحسابية)

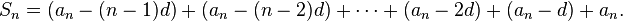
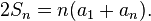

----------------------------------------------------
المصادر والمراجع :
* الموسوعة الحرة ويكيبيديا - النسخة الانكليزية , ترجمة : فريق موقع ومنتدى عالم الرياضيات .
* كتاب رياضيات عامة 1 - الدكتور حسن يوسف - منشورات جامعة البعث
أيضاً تسمى #المتتابعة و #المتوالية والتناسب .
تعريفها : هي مجموعة من الأغراض أو الأحداث المرتبة بنمط خطي حيث يكون ترتيب أعضاء المتتالية محددا تماما ومميزا. هذه الأعضاء تسمى عناصر المتتالية أو حدودها.
-----------------
تعريف رياضي : تسمى كل #دالة معرفة على مجموعة الأعداد الطبيعية متتالية .
فإذا كنا مستقر هذه التطبيق مجموعة الأعداد الحقيقية R سميت متتالية حقيقية .
وإذا كنا مستقر هذه التطبيق مجموعة الأعداد العقدية C سميت متتالية عقدية .
أما في مجموعة الدوال فتسمى متتالية دالية أو متتالية دوال .... وهكذا .
-----------------
مثلا (أ، ب، ج) متتالية مختلفة عن (ب، ج، أ) والاختلاف أساسا هنا هو في ترتيب عناصر المتتالية.
يمكن للمتتالية أن تكون منتهية كما هو الحال في المثال السابق أو غير منتهية مثل متتالية الأعداد الطبيعية : 1، 2، 3،...
------------------
#المتتاليات_العددية :
يمكن أن تعتبر المتتالية أيضا دالة رياضية منطلقها مجموعة الأعداد الطبيعية ومستقرها مجموعة عناصر المتتالية :
بمعنى أنها دالة تربط كل عنصر في مجموعة ما بترتيب معين يدل عليه عدد طبيعي : (f : N → X)
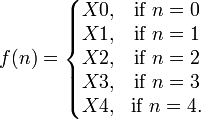
.
بهذا نكون قد قمنا عن طريق الدالة بترتيب أعضاء المجموعة X حسب الترتيب x0x1,x2...., حيث تدعى الأعداد 0، 1، 2،... دليل المتتالية.
----------------------------------------------------------
نرمز للمتالية بحرف بين قوسين مثل (a) .
يسمى a1 الحد الأول للمتتالية .
ويسمى a2 الحد الثاني للمتالية . .....
..... وهكذا
حتى نصل إلى an الحد العام للمتالية أو الحد النوني .
---------------------------------------------------------
#المتتالية_الحسابية :
في الرياضيات، متتالية حسابية هي متتالية من الأعداد حيث يكون الفرق بين أي حدين متتالين ثابتا.
على سبيل المثال فإن 3، 5، 7، 9، 11، 13، … هي متتالية حسابية لها أساس يساوي 2. أي أنّ 3، 5، 7 هي حدود من هذه المتتالية و الأساس 2 هو العدد المضاف بين كل حدّين متتاليين.
إذا كان الحد الأول من المتتالية الحسابية هو a1 و الفرق بين حدين متتاليين هو d عندها يعبر عن الحد ذي الترتيب n من متتالية حسابية بالعلاقة التالية:

أو بشكل عام

مثال
المتتالية 1 ،-3 ،-7، -11,.... حدها الأول هو 1 وأساسها هو 4- لأن الفرق بين حدين متتابعين يساوي دائما 4. وحتى نحصل على d نطرح كل حد من سابقه كالتالي:

لايجاد الحد النوني العشرين على سبيل المثال، تُطبق المعادلة السابقة :
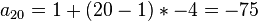
--------------------------------------------------
مجموع متتالية حسابية : (مهم جدا لمعرفة تقارب أو تباعد المتتالية لحسابية)

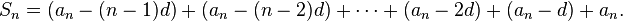
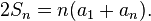

----------------------------------------------------
المصادر والمراجع :
* الموسوعة الحرة ويكيبيديا - النسخة الانكليزية , ترجمة : فريق موقع ومنتدى عالم الرياضيات .
* كتاب رياضيات عامة 1 - الدكتور حسن يوسف - منشورات جامعة البعث




» أنشطة ضرورية لحياة جامعية أكثر متعة وفائدة
» تحليل عقدي 2 سلالم ودورات من 2014 حتى 2016 فصل أول
» معادلات فيزيائية سلالم تصحيح من 2009 وحتى 2014
» فريق جامعة البعث بالميني فوتبول بطل الجامعات 2016
» امتحانات جامعة البعث الفصل الثاني 2016
» دليل أفكار البنى الجبرية 2
» بنى جبرية 2 - سلالم تصحيح
» حدسية بوانكاريه
» غربال إراتوستينس
» نظرية الشواش
» طبولوجيا مدخل وتعريف